Difference between revisions of "Plate buckling"
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
= Eigenvalue methods for computing buckling loads = | = Eigenvalue methods for computing buckling loads = | ||
Plate and shell buckling loads are classically computed by solving the eigenvalue problem <math> \mathbf{K} - \lambda \mathbf{G}(\mathbf{N}) </math> where <math> \mathbf{K}</math> is the shell's/plate's stiffness and <math> \mathbf{G}(\mathbf{N}) </math> is its geometric stiffness, dependent on the in-plane (membrane) | Plate and shell buckling loads are classically computed by solving the eigenvalue problem <math> \mathbf{K} - \lambda \mathbf{G}(\mathbf{N}) </math> where <math> \mathbf{K}</math> is the shell's/plate's stiffness and <math> \mathbf{G}(\mathbf{N}) </math> is its geometric stiffness, dependent on the in-plane (membrane) stress resultants <math>\mathbf{N}</math>, and <math> \lambda </math> is the proportional load factor. | ||
To compute the buckling load in FEAP, one first solves for the membrane stresses and shell stiffness, then one forms the geometric stiffness, and finally one uses an eigensolver to determine the buckling load(s). | To compute the buckling load in FEAP, one first solves for the membrane stresses and shell stiffness, then one forms the geometric stiffness, and finally one uses an eigensolver to determine the buckling load(s). | ||
| Line 13: | Line 13: | ||
As an example consider a cantilevered plate that is subjected to an in-plane compression, the buckling factor can be computed from the following input file. | As an example consider a cantilevered plate that is subjected to an in-plane compression, the buckling factor can be computed from the following input file. | ||
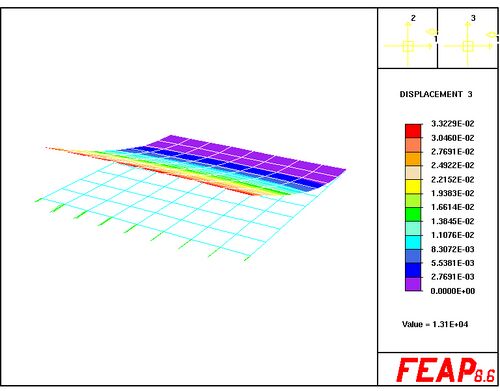
With this | With this coarse mesh the minimum eigenvalue is found to be <math>1.30888\times 10^4</math>. Thus the buckling force is found to be <math> \bar{p}\times w \times\lambda_{min}= 10^{-3} \times 0.1375 \times 1.30888\times 10^4 = 1.8</math> in the units of the input file. Note <math>\bar{p}</math> is the magnitude of the applied traction (Force per unit length) in the input file and <math>w</math> is the length of the edge of the plate. The validity of the result can be checked using the Euler load <math> P_\mathrm{euler} = \frac{1}{4}\frac{\pi^2 E h^3}{12(1-\nu^2)w}=1.9</math>. | ||
<pre> | <pre> | ||
feap * * Buckling of cantilever plate with a in-plane compression * * | |||
ndm = 3 ! 3 spatial dimensions | |||
ndf = 6 ! 6 dofs per node | |||
nen = 4 ! 4 nodes per element | |||
PARAmeters | |||
h = 0.001375 ! Thickness | |||
e = 436.4*10^6 ! Young's modulus | |||
nu = 0.3 ! Poisson's ratio | |||
w = 0.1375 ! side length | |||
MATErial | |||
SHELl | |||
ELAStic isotropic e nu | |||
THICk plate h 1 ! Shear factor set to 1 | |||
penalty drill e*1e-6 ! drill stiffness used for flat shells | |||
BLOCk | |||
CART 8 8 | |||
1 0 0 0 | |||
2 w 0 0 | |||
3 w w 0 | |||
4 0 w 0 | |||
CSURface ! Uniform force unit length on edge | |||
LINEar | |||
1 w 0 0.0 -1.0d-3 | |||
2 w w 0.0 -1.0d-3 | |||
EBOUndary ! Clamped edge | |||
1 0 1 1 1 1 1 1 | |||
END | |||
BATCH | |||
TANGent,,1 ! Linear problem no need to iterate | |||
GEOM ! Form geomteric tangent once stress-state is known | |||
SUBSpace,,5 ! Compute eigenvalues | |||
PLOT PERSpective | |||
PLOT HIDE | |||
PLOT MESH ! Show the mesh | |||
PLOT LOAD 1 ! Plot load with arrow head at node | |||
PLOT DEFOrmed,,,1e-5,1 ! Plot eigvecs with 1e-5 scaling and no re-scale to ref. config | |||
PLOT EIGVector,1,,3 ! Plot EigVec 1 with contours of 3-displacement | |||
END | |||
INTEractive | |||
STOP | |||
</pre> | </pre> | ||
[[File:FeapPlateBuck.jpg|center|500px]] | |||
Latest revision as of 11:39, 29 June 2023
Eigenvalue methods for computing buckling loads
Plate and shell buckling loads are classically computed by solving the eigenvalue problem where is the shell's/plate's stiffness and is its geometric stiffness, dependent on the in-plane (membrane) stress resultants , and is the proportional load factor.
To compute the buckling load in FEAP, one first solves for the membrane stresses and shell stiffness, then one forms the geometric stiffness, and finally one uses an eigensolver to determine the buckling load(s).
The basic MARCO commands are as follows:
TANGent,,1 GEOMetric SUBSpace,,5
Optionally one can use ARPAck,,5 (if optionally built).
As an example consider a cantilevered plate that is subjected to an in-plane compression, the buckling factor can be computed from the following input file. With this coarse mesh the minimum eigenvalue is found to be . Thus the buckling force is found to be in the units of the input file. Note is the magnitude of the applied traction (Force per unit length) in the input file and is the length of the edge of the plate. The validity of the result can be checked using the Euler load .
feap * * Buckling of cantilever plate with a in-plane compression * *
ndm = 3 ! 3 spatial dimensions
ndf = 6 ! 6 dofs per node
nen = 4 ! 4 nodes per element
PARAmeters
h = 0.001375 ! Thickness
e = 436.4*10^6 ! Young's modulus
nu = 0.3 ! Poisson's ratio
w = 0.1375 ! side length
MATErial
SHELl
ELAStic isotropic e nu
THICk plate h 1 ! Shear factor set to 1
penalty drill e*1e-6 ! drill stiffness used for flat shells
BLOCk
CART 8 8
1 0 0 0
2 w 0 0
3 w w 0
4 0 w 0
CSURface ! Uniform force unit length on edge
LINEar
1 w 0 0.0 -1.0d-3
2 w w 0.0 -1.0d-3
EBOUndary ! Clamped edge
1 0 1 1 1 1 1 1
END
BATCH
TANGent,,1 ! Linear problem no need to iterate
GEOM ! Form geomteric tangent once stress-state is known
SUBSpace,,5 ! Compute eigenvalues
PLOT PERSpective
PLOT HIDE
PLOT MESH ! Show the mesh
PLOT LOAD 1 ! Plot load with arrow head at node
PLOT DEFOrmed,,,1e-5,1 ! Plot eigvecs with 1e-5 scaling and no re-scale to ref. config
PLOT EIGVector,1,,3 ! Plot EigVec 1 with contours of 3-displacement
END
INTEractive
STOP