Branch Switch
Branch switch in FEAP is possible if one use arclength continuation methods. Here is a simple example. Consider a built-in column with an axial load.
feap ** Buckling Path Following with Arclength ** 0 0 0 3 3 8 para e = 1.0 d = 0.5 h = 20 pi = 4.*atan(1.) i = 16.*d*d*d*d/12 pe = pi*pi*e*i/h/h/4 ! Euler load p = 0.1*pe/4/d/d ! Reach euler load a prop value of 1 mate solid elastic moon e 0.4 0.05 finite mixed block cart 4 4 20*2 1 -d -d 0 2 d -d 0 3 d d 0 4 -d d 0 5 -d -d h 6 d -d h 7 d d h 8 -d d h eboun ! Fixed base 3 0 1 1 1 csur ! Pressure load (dead) surface 1 -d -d h -p 2 d -d h -p 3 d d h -p 4 -d d h -p end
As set up the buckling load occurs according to Bernoulli-Euler theory when the load factor reaches 10. If one simply applies the load in FEAP to this level and beyond the computed solution will just be a compression of the column, though above a load of 10, FEAP will report
*D4TRIU WARNING* Sign of diagonal changed when reducing 2 equations.
due to the two lowest buckling modes. As the load increases more modes can present themselves and more equations will be reported to have sign changes during the solution process. Though FEAP detects the multiple solutions it will typically only find the unstable vertical solution. One solution to this problem is to perturb the geometry slightly so that the problem does not actually have a bifurcation point. This can be quite effective but in many cases this is not a desirable methodology. FEAP, however, provides a second method that does not require perturbing a problems definition. In order to jump onto actual bifurcation branches one can use ARCLength and the ADD feature.
The basic process is to run the load up to where the bifurcation point is thought to be. Then after solving on to the suspected unstable branch, one computes the lowest eigenvector. This is then added to the current solution and the problem is re-solved (without increasing the load). If the eigenvector points in the direction of a bifurcation solution, one will likely converge upon it. Once on the bifurcation solution, if it is stable, increases in load should stay on the new path (without the need for guidance from further eigenvectors).
With the example give above, one can perform this process with the following algorithm
batch opti ! Optimize the equation ordering for the profile solver tplo ! Set up time-history plots end arcl 1 1 ! Save the arclength parameter (load) to file disp 1025 1 ! Save the corner x displacement disp 1025 2 ! Save the corner y displacement show batch dt,,1 arcl,,2 ! Initiate ARCLength loop,,10 ! 10 steps to get near buckling load time loop,,30 tang,,1 next plot,pview ! Save the state for paraview plotting next ! loop,,2 ! 1 Steps using the eigen method to probe for a bifurcation path time loop,,30 tang,,1 next iden subs ! Get eigenvalues and vectors arcl,add,1,.1 ! Pertub onto first eigenvector hope it is the stable branch loop,,30 ! Re-converge tang,,1 next plot,pview ! Save the state for paraview plotting next ! loop,,5 ! Take 5 more steps on hopefully the stable buckling branch time loop,,30 tang,,1 next plot,pview ! Save the state for paraview plotting next end inte stop
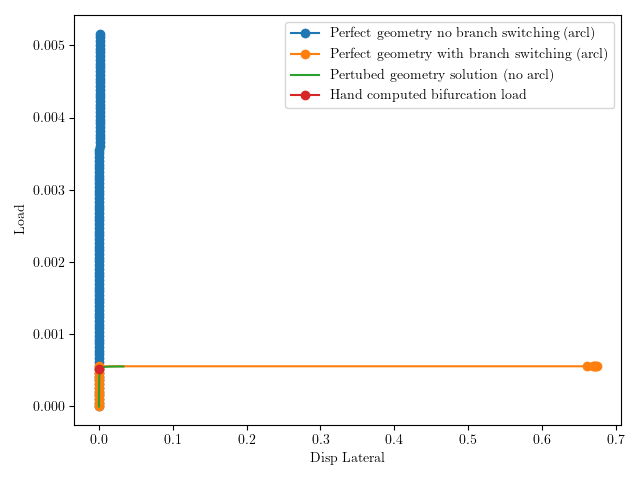
Here is a comparison of the solution techniques just mentioned in terms of axial load versus transverse motion (via cross plotting the data in the files Pxxxxa.dis and Pxxxxa.arc)
Here is an image of the bifurcated column.
The contents of the TPLOt files show that the bifurcation initiates at load step 11 (load = 10.0828) with a bifurcation in the x-direction. At load step 12 (load = 10.0929) the column lurches to the y-direction with some x-direction motion; note the cross-section is square and hence isotropic with respect to the area moment of inertia tensor. However at load step 13 (load = 10.0832) it stabilizes into a y-direction buckling.
| 0.0000E+00 | 0.0000E+00 |
| 1.0000E+00 | 0.0000E+00 |
| 2.0002E+00 | 0.0000E+00 |
| 3.0004E+00 | 0.0000E+00 |
| 4.0007E+00 | 0.0000E+00 |
| 5.0011E+00 | 0.0000E+00 |
| 6.0017E+00 | 0.0000E+00 |
| 7.0023E+00 | 0.0000E+00 |
| 8.0029E+00 | 0.0000E+00 |
| 9.0037E+00 | 0.0000E+00 |
| 1.0005E+01 | 0.0000E+00 |
| 1.0828E+01 | 0.0000E+00 |
| 1.0829E+01 | 0.0000E+00 |
| 1.0832E+01 | 0.0000E+00 |
| 1.0832E+01 | 0.0000E+00 |
| 1.0832E+01 | 0.0000E+00 |
| 1.0832E+01 | 0.0000E+00 |
| 1.0832E+01 | 0.0000E+00 |
| 0.0000E+00 | 0.0000E+00 | 0.0000E+00 |
| 1.0000E+00 | 1.0317E-05 | 1.0317E-05 |
| 2.0000E+00 | 2.0635E-05 | 2.0635E-05 |
| 3.0000E+00 | 3.0953E-05 | 3.0953E-05 |
| 4.0000E+00 | 4.1272E-05 | 4.1272E-05 |
| 5.0000E+00 | 5.1591E-05 | 5.1591E-05 |
| 6.0000E+00 | 6.1911E-05 | 6.1911E-05 |
| 7.0000E+00 | 7.2232E-05 | 7.2232E-05 |
| 8.0000E+00 | 8.2553E-05 | 8.2553E-05 |
| 9.0000E+00 | 9.2875E-05 | 9.2875E-05 |
| 1.0000E+01 | 1.0320E-04 | 1.0320E-04 |
| 1.1000E+01 | 9.1214E-02 | 1.1208E-04 |
| 1.2000E+01 | 9.2313E-02 | 6.6136E-01 |
| 1.3000E+01 | 1.1443E-04 | 6.6927E-01 |
| 1.4000E+01 | 1.1444E-04 | 6.7049E-01 |
| 1.5000E+01 | 1.1445E-04 | 6.7171E-01 |
| 1.6000E+01 | 1.1445E-04 | 6.7294E-01 |
| 1.7000E+01 | 1.1446E-04 | 6.7416E-01 |