Loops in mesh input

Loops can be used in meshes to repeat commands. When used with incremented parameters, this becomes a powerful technique for meshing. Consider the geometry found in the paper M.M. Ameen, O. Rokoš, R.H.J. Peerlings, M.G.D. Geers, Size effects in nonlinear periodic materials exhibiting reversible pattern transformations, Mechanics of Materials, Volume 124, 2018, Pages 55-70, ISSN 0167-6636, https://doi.org/10.1016/j.mechmat.2018.05.011.

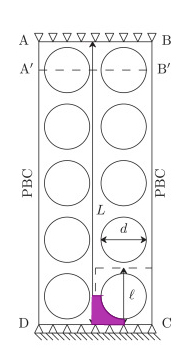
The geometry consists of a repeating pattern as shown in magenta.

If we have a mesh for the magenta region, we can repeatedly rotate it by 90 degrees to form a unit cell. Then we can loop those commands five times to shift the mesh upwards and twice laterally.

The easy way to generate the mesh for the magenta region is with super-nodes and blending, that way the curved surface can be made an exact circle.

snode
 1 0   l/2
 2 0   0
 3 l/2 0
 4 l/2 l/2
 5 l/2-d/2 l/2
 6 l/2-sqrt(2)*d/4 l/2-sqrt(2)*d/4
 7 l/2 l/2-d/2

side
 polar 5 6 4
 polar 6 7 4

followed by the commands to create the mesh (which we put in a second file called, say, Igeers2)

blend
surface na nt
quad
1 2 6 5
 
blend 
surface nt na 
quad
6 2 3 7

From here we create the unit mesh and then put loops around it to make the full mesh:

parameter
 l  = 9.97  ! mm
 nl = 5     ! repeats vertically
 d  = 8.67  ! mm
 na = 10    ! Arc discretization
 nt = 4     ! Thickness discretization
 ii = 0
 jj = 0

loop,2           ! Right/Left column

 loop,nl         ! Loop over vertical repeats

  transform       ! SW
   1 0 0
   0 1 0
   0 0 1
   -jj*l l*ii 0

  include,Igeers2 ! contains the bending commands from above

  transform       ! SE
   0 -1 0
   1  0 0
   0  0 1
   l-jj*l l*ii 0

  include,Igeers2

  transform       ! NE
   -1  0 0
    0 -1 0
    0  0 1
    l-jj*l  l+l*ii 0

  include,Igeers2

  transform       ! NW
    0 1 0 
   -1 0 0
    0 0 1
    0-jj*l l+l*ii 0

  include,Igeers2

  parameter
   ii = ii + 1

 next

 parameter 
  jj = jj + 1
  ii = 0

next

The full file for the analysis looks like; this version will provide a solution that goes past the bifurcation point in the problem and remains on the unstable branch. To see the stable (bifurcated) solution, one needs to employ branch switching.

If on looks in the output file one will see the tangent stiffness progressively develops a saddle-point structure (negative eigenvalues which represent bifurcations branches).

** Ameen, Rokos, Peerlings, Geers; Mech Mat; 2008 **
feap
0 0 0 2 2 4

parameter
 m1 = 0.55  ! MPa == N/mm^2 (ARPG)
 m2 = 0.30  ! MPa == N/mm^2 (ARPG)
 k1 = m2/m1 ! Yeoh parameters for FEAP
 k2 = 0.d0  ! Yeoh parameters for FEAP
 kk = 55    ! MPa == N/mm^2 (ARPG)
 mu = 2.d0*m1
 ee = 9.d0*kk*mu/(3.d0*kk+mu)
 nu = (ee-2.d0*mu)/(2.d0*mu)
 l  = 9.97  ! mm
 nl = 5     ! repeats vertically
 d  = 8.67  ! mm
 na = 10    ! Arc discretization
 nt = 4     ! Thickness discretization
 ii = 0
 jj = 0

mate
 solid
 finite volume 1
 elastic yeoh ee nu k1 k2


snode
 1 0   l/2
 2 0   0
 3 l/2 0
 4 l/2 l/2
 5 l/2-d/2 l/2
 6 l/2-sqrt(2)*d/4 l/2-sqrt(2)*d/4
 7 l/2 l/2-d/2

side
 polar 5 6 4
 polar 6 7 4


loop,2           ! Right/Left column

 loop,nl

  transform       ! SW
   1 0 0
   0 1 0
   0 0 1
   -jj*l l*ii 0

  include,Igeers2

  transform       ! SE
   0 -1 0
   1  0 0
   0  0 1
   l-jj*l l*ii 0

  include,Igeers2

  transform       ! NE
   -1  0 0
    0 -1 0
    0  0 1
    l-jj*l  l+l*ii 0

  include,Igeers2

  transform       ! NW
    0 1 0 
   -1 0 0
    0 0 1
    0-jj*l l+l*ii 0

  include,Igeers2

  parameter
   ii = ii + 1

 next
 
 parameter 
  jj = jj + 1
  ii = 0

next


eboun
 2 0     1 1
 2 nl*l  1 1 


edisp
 2 nl*l  0 -0.1*nl*l


end

tie

elink
 1 -l l


batch
 opti
 dt,,0.01
 prop,,1
 plot,defo
end


batch
 loop,,100
  time
   loop,,20
    tang,line,1
   next
   plot wipe
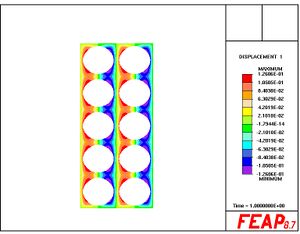
   plot cont 1,,1
   iden
   subs,,5
 next
end


inte
stop