Loops in mesh input
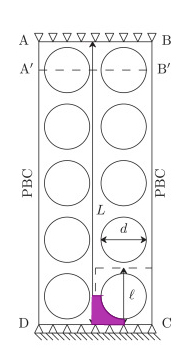
Loops can be used in meshes to repeat commands. When used with incremented parameters, this becomes a powerful technique for meshing. Consider the geometry found in the paper M.M. Ameen, O. Rokoš, R.H.J. Peerlings, M.G.D. Geers, Size effects in nonlinear periodic materials exhibiting reversible pattern transformations, Mechanics of Materials, Volume 124, 2018, Pages 55-70, ISSN 0167-6636, https://doi.org/10.1016/j.mechmat.2018.05.011.
The geometry consists of a repeating pattern as shown in magenta.
If we have a mesh for the magenta region, we can repeatedly rotate it by 90 degrees to form a unit cell. Then we can loop those commands five times to shift the mesh upwards and twice laterally.
The easy way to generate the mesh for the magenta region is with super-nodes and blending, that way the curved surface can be made an exact circle.
snode 1 0 l/2 2 0 0 3 l/2 0 4 l/2 l/2 5 l/2-d/2 l/2 6 l/2-sqrt(2)*d/4 l/2-sqrt(2)*d/4 7 l/2 l/2-d/2 side polar 5 6 4 polar 6 7 4
followed by the commands to create the mesh (which we put in a second file called, say, Igeers2)
blend surface na nt quad 1 2 6 5 blend surface nt na quad 6 2 3 7
From here we create the unit mesh and then put loops around it to make the full mesh:
parameter
l = 9.97 ! mm
nl = 5 ! repeats vertically
d = 8.67 ! mm
na = 10 ! Arc discretization
nt = 4 ! Thickness discretization
ii = 0
jj = 0
loop,2 ! Right/Left column
loop,nl ! Loop over vertical repeats
transform ! SW
1 0 0
0 1 0
0 0 1
-jj*l l*ii 0
include,Igeers2 ! contains the bending commands from above
transform ! SE
0 -1 0
1 0 0
0 0 1
l-jj*l l*ii 0
include,Igeers2
transform ! NE
-1 0 0
0 -1 0
0 0 1
l-jj*l l+l*ii 0
include,Igeers2
transform ! NW
0 1 0
-1 0 0
0 0 1
0-jj*l l+l*ii 0
include,Igeers2
parameter
ii = ii + 1
next
parameter
jj = jj + 1
ii = 0
next
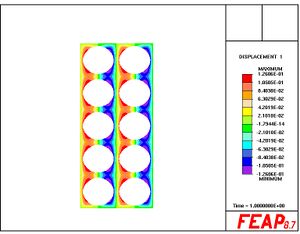
The full file for the analysis looks like; this version will provide a solution that goes past the bifurcation point in the problem and remains on the unstable branch. To see the stable (bifurcated) solution, one needs to employ branch switching.
If on looks in the output file one will see the tangent stiffness progressively develops a saddle-point structure (negative eigenvalues which represent bifurcations branches).
** Ameen, Rokos, Peerlings, Geers; Mech Mat; 2008 **
feap
0 0 0 2 2 4
parameter
m1 = 0.55 ! MPa == N/mm^2 (ARPG)
m2 = 0.30 ! MPa == N/mm^2 (ARPG)
k1 = m2/m1 ! Yeoh parameters for FEAP
k2 = 0.d0 ! Yeoh parameters for FEAP
kk = 55 ! MPa == N/mm^2 (ARPG)
mu = 2.d0*m1
ee = 9.d0*kk*mu/(3.d0*kk+mu)
nu = (ee-2.d0*mu)/(2.d0*mu)
l = 9.97 ! mm
nl = 5 ! repeats vertically
d = 8.67 ! mm
na = 10 ! Arc discretization
nt = 4 ! Thickness discretization
ii = 0
jj = 0
mate
solid
finite volume 1
elastic yeoh ee nu k1 k2
snode
1 0 l/2
2 0 0
3 l/2 0
4 l/2 l/2
5 l/2-d/2 l/2
6 l/2-sqrt(2)*d/4 l/2-sqrt(2)*d/4
7 l/2 l/2-d/2
side
polar 5 6 4
polar 6 7 4
loop,2 ! Right/Left column
loop,nl
transform ! SW
1 0 0
0 1 0
0 0 1
-jj*l l*ii 0
include,Igeers2
transform ! SE
0 -1 0
1 0 0
0 0 1
l-jj*l l*ii 0
include,Igeers2
transform ! NE
-1 0 0
0 -1 0
0 0 1
l-jj*l l+l*ii 0
include,Igeers2
transform ! NW
0 1 0
-1 0 0
0 0 1
0-jj*l l+l*ii 0
include,Igeers2
parameter
ii = ii + 1
next
parameter
jj = jj + 1
ii = 0
next
eboun
2 0 1 1
2 nl*l 1 1
edisp
2 nl*l 0 -0.1*nl*l
end
tie
elink
1 -l l
batch
opti
dt,,0.01
prop,,1
plot,defo
end
batch
loop,,100
time
loop,,20
tang,line,1
next
plot wipe
plot cont 1,,1
iden
subs,,5
next
end
inte
stop